A group of us here at Hanapin recently participated in a free 21-Day Excel Course directed by renowned Microsoft Excel expert Dr. Wayne Winston. The course itself felt slow at first, but ultimately revealed several Excel capabilities I’d never known. Most exciting of these, to me, is the capacity to regress multiple variables without an advanced statistical software (such as STATA). In this post, I’ll share the step-by-step for setting up and running regressions in Excel, and how this tool can help in your PPC analyses and account management.
Excuse Me, I Regress
Before we dig into the technical implementation, you might be wondering to yourself, “What in the world is a regression?” In short, regressions look at the relationships between variables. For any dependent variable (“Y”), what set of independent variables (“Xs”) contribute to the variation Y, and how much of that behavior does the regression model explain? (See here for an in-depth review of regression analyses)
Linear regressions (or multiple linear regressions) are the most common, fitting into a summed equation of the form:
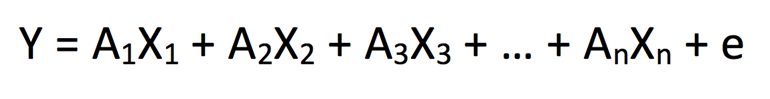
where Y is the dependent variable, X1 – Xn represent a set of n independent variables and A1 – An are the coefficient constants corresponding to X1 – Xn. This is basic statistical model-building, and so we recognize that there will be some inconsistency between our predicted and observed outcomes for each “y” iteration. Thus, the error term “ + e” is added to account for such variance.
Why Regress In PPC?
Regressions can be used in any number of analyses. For instance, you might want to consider what effect CPC bid changes have on Avg. Position, Lost Impression Share, or Quality Score. You may examine which element (expected CTR, landing page experience, or ad relevance) has the strongest impact on your account-, campaign-, or keyword-level Quality Score. Perhaps, as we will see in the below example, you want to uncover the role that Search and Display CPCs and Conversion Rates are playing in the overall CPA for your account.
Whatever your end goal is, the process for setting up and determining the value of your regression model is the same.
Step 1: Prepare Your Data
As with any analysis, a good result requires quality data that has been correctly prepped. For good regression results, you need a sufficient amount of data (at least as many data points as the number of independent variables, but the more data you have available, the more accurate your regression model can be). To increase the number of data points, you might consider segmenting your data by day, week, or month (depending on the time frame being examined).
For our example, we are using data from the past 24 months in Adwords. After downloading a campaign report (segmented by month), we create a pivot table to examine Clicks, Cost, and Conversions by month and Campaign type:
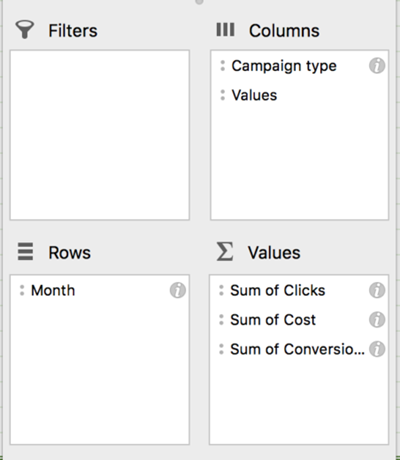
From here, we can calculate CPA, CPC, and CVR for each network, as well as Total CPA. Then it’s just one quick copy-and-paste of the data into a new sheet, we are ready to start regressing!
Step 2: Build Your Model (Choosing Variables)
Model building has two main components: thoughtful planning and flexible revision. Thoughtful planning is about considering which variables would be the best fit for your model logically (and what data is available for use). Spending a little extra time in the planning stage can save you time and sanity later as you test and retest your model. Even with careful preparation, you may still need to flexibly revise your model as you regress and identify variables that are significant and not.
Two important notes when selecting independent variables:
- Independent variables should have a conceivable, logical relationship to the dependent variable (i.e. avg. rainfall in Tokyo and # of heart attacks in Wisconsin would be low on my list of correlations to examine)
- Independent variables should not be highly correlated to each other (i.e. including Cost, Clicks, and CPC as independent variables within the same regression would cause a multicollinearity error in the model)
In our example, we want to look at what is driving our account CPA. We know that there are two networks on which we run ads in Adwords—Search and Display—and we know that the two main variables driving CPA (Cost/Conversion) for each network are CPC (Cost/Click) and CVR (Conversion/Click).
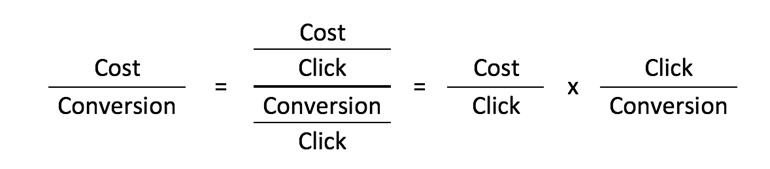
Therefore, we will begin by regressing CPA on CPC and CVR for Search and Display separately to determine which independent variables are significant, and thus should be included in our final model.
Step 3: Regress And Revise
To run a regression in Excel:
1. Before initiating the regression in Excel, first check to make sure that the independent variables (data columns) are neighboring each other.
2. Next, confirm that the “Analysis ToolPak” Add-on is enabled for Excel (visible in the “Data” ribbon once enabled).
3. Within the Data Analysis toolbox, select “Regression.”
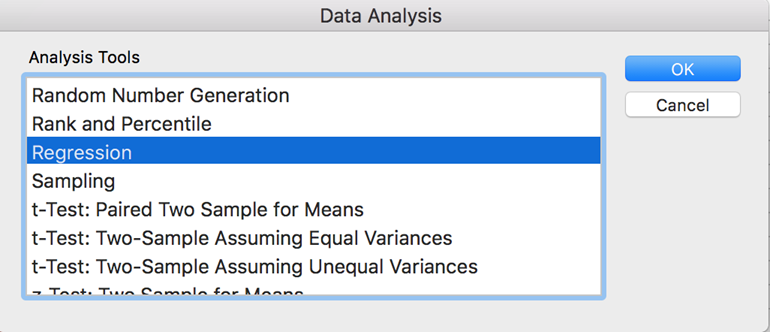
4. Input your Dependent Variable (Y) range, and Independent Variables (X) range, selecting “Labels” if you choose to include the column headers
5. Select a placement for your regression output (a new or existing worksheet)
6. Select “residuals” if you want to check for and remove outliers in the data
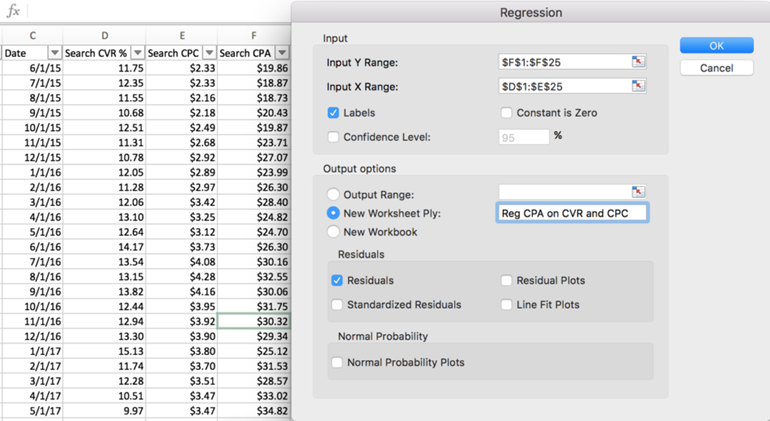
7. Click “OK” to run the regression. You will automatically be navigated to the sheet containing the output summary and details.
8. If examination of the regression output reveals insignificant independent variables (typically, p-values is greater than .1) or a lower-than-expected R-squared (see “A” below), you can repeat the process as needed to refine the model.
Step 4: Understanding The Output
Looking at a Summary Output for the first time can be intimidating and discouraging. To make it easier, highlighted below are key sections of the output to help you assess the model your regression just built.

(A) R Square and Adjusted R Square: This is a measure of how well your model “fits” the data. In short, R Square tells how much of the variation in Dependent Variable is explained by the chosen Independent Variables. Adjusted R Square is basically the same, but also considers the number of Independent Variables included, providing a slightly more accurate measure. (There is no such thing as a “good” or “right” R Square, as it depends on the type of model and data you are using, but the higher the better).
(B) Standard Error: The square root of the sum of squared differences between the predicted and actual results. For a normal distribution, roughly 65% of residuals (see “E” below) will be less than one Standard Error and 95% will be less than 2. Residuals greater than twice the Standard Error are typically labeled as outliers in the data.
(C) Coefficients of Independent Variables: Coefficients are the “A” terms in your regression formula. Thus, for this example, a 1-unit increase in CPC should equal an 8.4 increase in CPA (assuming CVR remains constant).
(D) P-value of Independent Variables: In layman’s terms, P-value tells the significance of the independent variable. Low P-values are significant (aiming for less than .1), while high P-values indicant the perceived correlation could be pure chance. Independent Variables with high P-values should be excluded during the “flexible revision” stage.
(E) Residuals: This shows the difference between the predicted value of the Dependent Variable for each iteration and the actual recorded value. As mentioned above, most residuals should be less than 1 Standard Error and nearly all should be less than the value of 2 * Standard Error. You can decide whether to include or exclude any identified outliers (residuals greater than twice the Standard Error) from your model.
Step 5: Putting It Together (The Takeaways Part!)
After running three regressions, we found the following three equations relating Search and Display CPC and CVR to network and Total CPAs:



These equations verify what we already knew (or thought we did): that Search and Display CPCs and CVRs are all playing a significant role in the behavior of our Total CPA. Beyond that, however, they also revealed 3 things that a standard heat map would not.
- An increase in Search CPC has 3.5x the impact on Search CPA than an equivalent lift in Search CVR
- Fluctuations in Display CPC have nearly 5x the impact of Display CVR on Display CPA
- Overall, shifts in Display network performance affect Total CPA more dramatically than shifts of a similar magnitude in Search network performance
From this, it’s clear that Display CPC is the #1 target for optimization if I’m aiming to reduce Total CPA. Search CPC and Display CVR are next, with Search CVR the least of my priorities.
Regressions are a powerful tool and a great addition to the PPC Manager’s tool belt. This basic example shows just one of many ways that regressions can help you understand the relationships between your beloved KPIs. We hope that you’ll test out or continue using the regression capability in Excel, and share your experience/thoughts/findings with us on Twitter!



